Los sistemas numéricos y alfabéticos

    son conjuntos de números/letras y reglas de generación que permite construir todos los números validos. empezando con este tema primero entenderemos que es un numero decimal, binario y hexadecimal con un corto video en YouTube:

 

Si entendemos que en binario no se pueden usar más números que 1 y 0 es el estilo de código, entonces en decimal los números generales son del 1 al infinito y en hexadecimal los números del 1 al 9 y de la A a la f.

el numero 15 en el sistema binario es 1111 y en el sistema hexadecimal es F.

Ejemplo queremos convertir el número 28 a binario:

28 dividimos entre 2 : Resto 0
14 dividimos entre 2 : Resto 0
7 dividimos entre 2 : Resto 1
3 dividimos entre 2 : Resto 1 y cociente final 1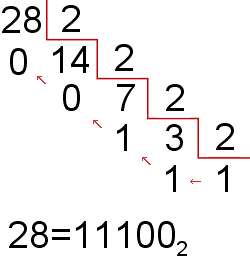

Entonces el primer número del número equivalente en binario sería el cociente último que es 1 y su resto que es también 1, la tercera cifra del equivalente sería el resto de la división anterior que es 1, el de la anterior que es 0 y el último número que cogeríamos sería el resto de la primera división que es 0.

Con todos estos número quedaría el número binario: 11100.

Conclusión el número 28 es equivalente en binario al 11.100.

A continuación, explicamos cómo pasar un número del sistema decimal al sistema octal, y viceversa.

Cambio de base 10 a base 8

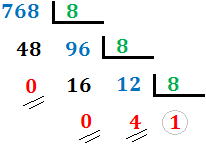
Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto).

En nuestro caso,

• El último cociente es 1.

• El último resto es 4.

• El penúltimo resto es 0.

• El primer resto es 0.

• Por tanto, el número 768 en base octal es 1400. Es decir,  

Un número octal se puede convertir rápidamente a su equivalente decimal multiplicando cada número octal por su peso posicional. Ejemplo:

• 3828 = 4 * (82) + 8 * (81) + 2 * (80)
• = 3 * 64 + 8 * 8 + 2 * 1
• = 25810